Unit Test Review: Trigonometry

Unit Test Review

~Trigonometry~

This blog post is a list of many of the key concepts that students should understand by the end of the trigonometry unit. 

Chapter 7

• Rates, Ratios and Proportions
• Solving Proportions (Cross multiplication & isolation)
• Angle Relationships
• CAT, SAT, OAT, IST, SATT, EAT, PTL-F Pattern, PTL-C Pattern and PTL-Z Pattern
• The Pythagorean Theorem
• Two Properties of Similar Triangles
• Finding corresponding angles and corresponding sides in two similar triangles. 
• Proportionality Statements
• Scale Factor (k)
• Primary Trigonometric Ratios
• Labeling hypotenuse, opposite side and adjacent side in respect to a reference angle
• The Tangent Ratio: solving for unknown angles and unknown sides
• The Cosine Ratio: solving for unknown angles and unknown sides
• Ratio cannot be greater than 1 (i.e., denominator is always greater than numerator).
• The Sine Ratio: solving for unknown angles and unknown sides
• Ratio cannot be greater than 1 (i.e., denominator is always greater than numerator).
• SOH CAH TOA
• Angle of Elevation (inclination)
• Angle of Depression 

Chapter 8

• "Solving the Triangle"
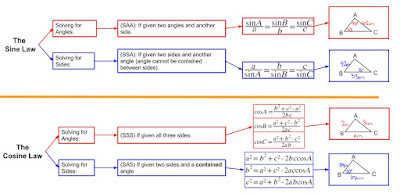
• The Sine Law: solving for unknown angles and unknown sides
• The Cosine Law: solving for unknown angles and unknown sides
• The Sine Law vs. The Cosine Law 

Chapter 7 & 8

• Solving Problems Using Trigonometry 
• Formulas for Trigonometry

Reviewing Sine Law and Cosine Law

Reviewing The Sine Law and The Cosine Law

The following diagram summaries the varies ways we can apply the sine law and cosine law in solving for unknown angles and sides in non-right triangles (click the image to enlarge it.)

The Sine Law vs. The Cosine Law. Created by Mike Studenny.

Trigonometry - The Cosine Law - Solving for Angles

The Cosine Law - Solving for Angles

We have been working on applying the cosine law to solve for unknowns in non-right triangles. The last video lesson and blog discussed how to apply the cosine law to solve for unknown side lengths. We know that to do this we need to be given any two sides and a contained angle between them. 

To solve for an unknown angle while using the cosine law we need to be given all three sides. 

The following is a example of the various ways we can arrange the cosine law in order to solve for each unknown angle of ∆ABC:

The Cosine Law - Solving for Angles. Created by Mike Studenny.

The important pieces to notice when using the cosine law and solving for angles can be summaries into a few key points:

• The equation is simply a rearranged version of the cosine law used to solve for sides.
• The equation still matches the unknown value on the left of the equation to it's partner on the far right (i.e., unknown angle A matches to given side a.)
• The equation contains the two other side lengths than the matching one. 
• These two other side lengths appear twice once in the numerator and once in the denominator. 

The video lesson that corresponds to this blog post explains how to apply the equation to isolate for the unknown angle. If you have a strong understanding of the primary trigonometric ratios and how to isolate for unknowns using them this math should not be too difficult. Generally, the hard part is developing the equations correctly. 

Follow the link below to access the video lesson:

Trigonometry - The Cosine Law - Solving for Angles

Trigonometry - The Cosine Law - Solving for Sides

The Cosine Law - Solving For Sides

This lesson works on a brand new equation. So far we have learnt how to solve for unknown sides only using the sine law. When solving for an unknown side the sine law requires the following:

• (ASA) Two angles and one side.

The problem with this is that we want to be able to solve problems that contains other sets of given information. Enter: The Cosine Law!

The cosine law allows us to solve for unknown sides of a triangle if given the following condition:

• Any two sides and a contained angle* 

The important thing about building your cosine law equation is to make sure that the left side's side variable matches the angle's variable at the end. The following are three examples of how to build various equations for ∆ABC. The first is to find side a. The second is to find side d. The third is to find side c. It's important to notice how each unknown side in the equation matches to a known angle in the right side of the equation. Also how the other two sides each appear twice per equation. 

The Cosine Law. Developed by Mike Studenny.

The corresponding lesson to this blog post goes into detail on how to apply the cosine law to solve for an unknown side. The process for solving the equation is outlined there. 

To view the video lesson follow the link below:

8.2 - Trigonometry - The Cosine Law - Solving for Sides 

Trigonometry - The Law of Sines - Word Problems

The Law of Sines - Word Problems

This lesson looks at how to apply the law of sines to a variety of word problems. When tackling these problems, here are a few steps to follow as a means of organizing your thoughts:

1. Read through the question from start to finish.
2. Pick out the important parts of the questions (I like to highlight or underline these)
3. Build and label your diagram.
4. Write out and fill in any given information into the Sine Law
5. Choose two ratios to set equivalent to each other to solve for one unknown value. 

Click the link below to access the video lesson:

8.1 The Law of Sines - Word Problems

Trigonometry - The Law of Sines

The Sine Law

This lesson looks at the development and preliminary applications of the Sine Law. The video lesson first works through the development of the algebraic proof for the Sine Law. This requires the prior understandings of the primary trigonometric ratio of Sine. This sine law is used on non-right angle triangles to solve for unknown angles or sides. The overlaying idea of how this sine law is derived is that we are cutting the triangle into two right angle triangles and using the sine ratio to solve for 2 of the three sides. We do this again to solve for a third side. This shows that all three ratios of sides lengths divided by the ratio of sine for the corresponding angle (to the side length) are equal to each other.

Through the investigative proof we found applying this ratio to be true.

Therefore, we are able to use the following ratio to solve for unknown angles and sides of non-right angle triangles. 

---

A quick summary of what information you need given in a problem to be able to solve for which known is shown below:

• The sine law can be used to find a side length of a non-right triangle if given two angles and one side length.

• The sine law can be used to find an angle of a non-right triangle if given two sides and one angle that is corresponds to one of the given sides (i.e., the angle cannot be contained by the given sides)

Follow the link below for the video of this lesson

8.1 - Trigonometry - The Law of Sines

Trigonometry - Solving Triangles - Real World Problems

Solving Triangles - Real World Problems

In this lesson we begin applying our understanding of the primary trigonometric ratios to real world problems. Thus far, we have been using the ratios to solve problems that pretty much occur only in the "math world." Personally, I find applying math to problems that arise in the real world is the most exciting part! During my own personal math journey I have found that as soon as you apply math to the real world it doesn't only give you answers to interesting questions but also gives you the tools to as questions that are even more interesting. 

For a number of these  questions we used two new definitions:

Angle of Elevation or Inclination: the angle between the horizontal and the line of sight from an observer's eye to some object above eye level.

Angle of Depression: The angle between the horizontal and the line of sight from an observer's eye to a point below eye level. 

When trying to apply our primary trig. ratios to real world problems there is a series of steps to follow as a means to organize the process:

1. Draw a diagram to represent the situation
2. Fill in all known information
3. Identify what needs to be calculated, side or angle
4. Solve for the unknown measure using a trig ratio
5. Write a concluding statement.

Following these steps will surely help make the real world, word problems much easier. Also, I have found that part of real world problems is that they result in a struggle. This struggle is not a bad thing. It is a natural part of working through math... allowing yourself to struggle yet not get disheartened will help you develop you skills in math. 

The following link is for the video lesson:

7.5 - Trigonometry - Solving Right Triangles In The Real World - PART ONE
7.5 - Trigonometry - Solving Right Triangles In The Real World - PART TWO